
https://www.coursera.org/learn/modernrobotics-course2-ko
현대 로봇공학, 강좌 2: 로봇 기구학
Northwestern University에서 제공합니다. 로봇이 어떻게 작동하는지 궁금하신가요? 로봇공학 커리어에 관심이 있으신가요?로봇공학의 모든 하위 분야에서 사용되는 기초적인 수학적 모델링 기법을
www.coursera.org
Inverse kinematics(IK): the calculation of the joint configuration from the end effector frame configuration(postion+orientation).
●For n-revolute joint serial robots, $T_{sb}\in SE(3)\longrightarrow \theta\in\mathbb{R}^{n}$
●Widely used representations:
●Unlike the forward kinematics of serial robots, it can have ①a unique solution, ②multiple solutions, or ③no solution
●Some systems like the 6R PUMA or the Standford arm have analytic IK solutions.
●Most systems don't have an analytical solution, or we can't find one. So, numerical methods are used.
└e.g. Newton-Raphson method, Method of optimization)
●Even in cases where an analytic solution exists, numerical methods are used to improve accuracy.
Newton-Raphson method: An iterative numerical method for finding a function's root using the only linear part of the Taylor series approximation.
●Main concept: Finding a guess error($\theta^{k+1}-\theta^{k}$) from the result error($x-g(\theta^{k})$). (My own explanation)
●Only one root is found at a single set of iterations, and the result depends on the initial root guess. (Root that is the closest to the initial guess)
●Three possibilities exist: ①Find the desired root, ②Find the undesired root, ③Fail to find root(Divergence)
●For a algebraic equation $g(\theta)=x_{d}$, initial root guess $\theta^{0}$ ($\theta,x_{d}\in \mathbb{R}$):
Repeating $\theta^{k+1}-\theta^{k}=\left(\frac{\partial g}{\partial \theta}(\theta^{k}) \right)^{-1} \left\{x- g(\theta^{k}) \right\}$
●For a matrix equation $g(\theta)=x_{d}$, initial root guess $\theta^{0}$ ($\theta,x_{d}\in \mathbb{R}^{n}$):
Repeating $\theta^{k+1}-\theta^{k}=J^{-1}(\theta^{k})\left\{x_{d}- g(\theta^{k}) \right\}$
(Moore-Penrose) Pseudo-inverse $A^{\dagger}$: A generalization of matrix inverse that exists for any matrix(even for non-square, singular matrix=noninvertible matrix).
For $A\in \mathbb{R}^{m\times n}$, $m\gt n$ (tall matrix), $A^{\dagger}=A^{T}(AA^{T})^{-1}$
For $A\in \mathbb{R}^{m\times n}$, $m\lt n$ (fat matrix), $A^{\dagger}=(AA^{T})^{-1} A^{T}$
●The matrix equation $Ax=b$ and the solution $x=A^{\dagger}b$ results in cases.
①If solutions exist, $x=A^{\dagger}b$ provides the solution with the smallest norm.
②If no solutions exist, $x=A^{\dagger}b$ provides the value that minimizes the error.
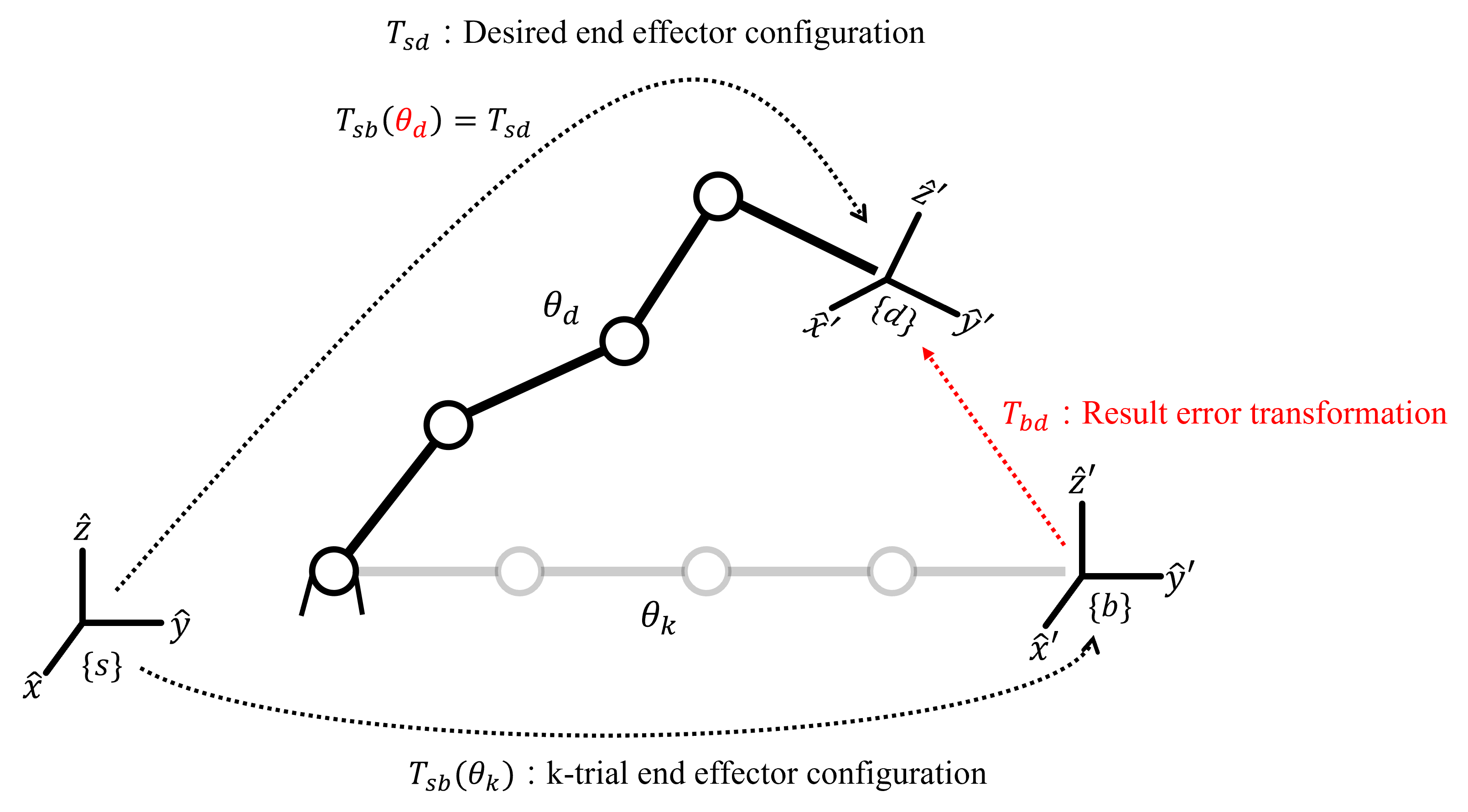
IK using Newton-Raphson method: Find a root of the IK matrix equation using the Newton-Raphson method.
●Main point: Convert result error transformation $T_{bd}\in SE(3)$ into result error twist $\nu\in\mathbb{R}^{6}$ with the matrix log of rigid-body motion.
$[\nu_{s}]=log(T_{bd}(\theta^{k}))=log(T_{sb}^{-1}(\theta^{k})T_{sd})$
●FK $T_{sb}(\theta)$ is needed.
Space frame: $\theta^{k+1}-\theta^{k}=J^{\dagger}_{s}(\theta^{k})\nu_{s}$
Body frame: $\theta^{k+1}-\theta^{k}=J^{\dagger}_{b}(\theta^{k})\nu_{b}$ (Generally used)
+)Modern Robotics book example 6.1 Matlab code.


Closed chain: Any kinematic chain that contains loops
●Delta robot, Stewart platform $\in$ Parallel mechanism $\in$ Closed chain
●Not all joints are actuated
●Joints satisfy loop-constraint-equations. This makes an additional Jacobian called Constraint Jacobian.
●As opposed to open chains, IK has a unique solution while FK can have multiple solutions.
========================================================================
정확한 정보 전달보단 공부 겸 기록에 초점을 둔 글입니다.
틀린 내용이 있을 수 있습니다.
틀린 내용이나 다른 문제가 있으면 댓글에 남겨주시면 감사하겠습니다. : )
========================================================================
'공부 > Modern Robotics' 카테고리의 다른 글
| [Modern Robotics] 강좌 3: 로봇 동역학 #2 (1) | 2024.12.11 |
|---|---|
| [Modern Robotics] 강좌 3: 로봇 동역학 #1 (0) | 2024.12.06 |
| [Modern Robotics] 강좌 2: 로봇 기구학 #1 (0) | 2024.11.29 |
| [Modern Robotics] 강좌 1: 로봇 동작의 기초 #2 (0) | 2024.11.25 |
| [Modern Robotics] 강좌 1: 로봇 동작의 기초 #1 (0) | 2024.11.16 |



